1491: 奇妙矩阵

emaster有一个 $n*m(n行m列)$ 的矩阵。初始矩阵的每个位置上的数都是 $1$ 。

我们以 $(i,j)$ 表示第 $i$ 行 $j$ 列。  
当且仅当如下两个条件都满足时我们可以花费一步将$(i,j)$上的数从 $0$ 变成 $1$ 或从 $1$ 变成 $0$ :

- $(i-1, j)$ 和  $(i, j-1)$ 上的数都为 $1$。
- $\forall (c, d) \in \{(c, d) \mid 1 \leq c \leq i, 1 \leq d \leq j, (c, d) \neq (i-1, j), (c, d) \neq (i, j-1), (c, d) \neq (i, j)\},\ (c, d)上的数 \text{都为 0}$。  


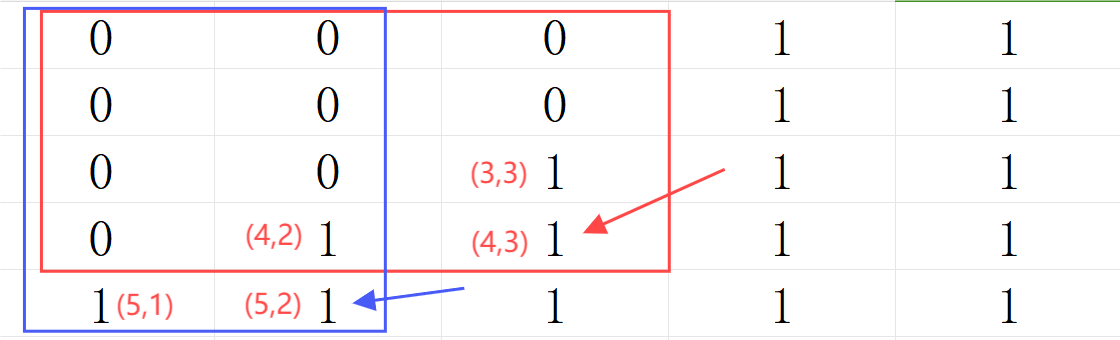
例如：图中是一个 $5*5$ 的矩阵，其中 $(4,3)$上的数可以进行更改, $(5,2)$ 上的数可以更改。当然， $(1,1)$ 也满足条件，可以更改。



emaster想知道矩阵上所有数变成 $0$ 最少需要多少步。这个答案可能很大，请你输出答案对$998244353$取模后的结果。

一行，两个整数，依次为$n,m$。

数据范围：  
$1 \le n,m \le 1000$

一行，一个整数。代表矩阵上所有数变成 $0$ 最少需要的步数。结果对$998244353$取模。

2 2

6