1423: 最伟大的巫师

巫师界将要评选谁是最伟大的巫师。

目前共 $n$ 位巫师参与选拔，我们将视为 $n$ 个点,每个点有其点权。

评委们给出了 $m$ 条看法,我们视为 $m$ 条有向边,每条看法有一定的认可度，我们视为该有向边的边权。

emaster心目中最伟大的巫师为 $1$ 号巫师，由于emaster赞助了本次比赛，他可以根据自身的认可度 $x$ 来删去或增加有向边，具体规则如下：

- 任意选择某个整数 $k(0 \le k \le x)$,删去所有认可度不高于 $k$ 的边。

- 若不存在以 $1$ 号点为起点，指向 $v$ 点的有向边，且emaster的认可度不低于 $v$ 点的点权 $w$ ，则可以增添这条边。

- 操作次数和操作顺序无限制。

为了使得 $1$ 号巫师夺冠的结果尽可能权威，要求最终生成的图中 $1$ 号点到任意点可达。且图中不存在环。

请你告诉emaster最低需要的认可度。

第一行，两个整数$n,m$，分别代表点与边的数量。

第二行，$n-1$个整数，第$i$个整数$a_i$代表第$i+1$号点的点权。

接下来$m$行，每行三个整数$u,v,w$，代表图中有一条以   $u$ 为起点， $v$ 为终点，边权为 $w$ 的有向边。

数据范围：

$1 \le n \le 10^5$

$0 \le m \le 10^5$

$1\le u,v \le n$

$1\le w,a_i \le 10^9$

此外，保证给出的图无重边，无自环，若有 $u$ 为起点、 $v$ 为终点的有向边，则不会给出 $v$ 为起点、 $u$ 为终点的有向边。

4 3
7 8 9
1 2 10
2 3 8
3 1 8

9

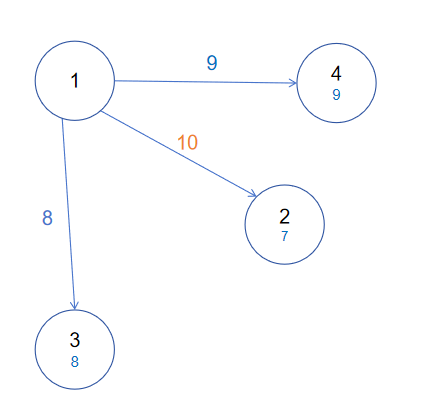
初始图如下

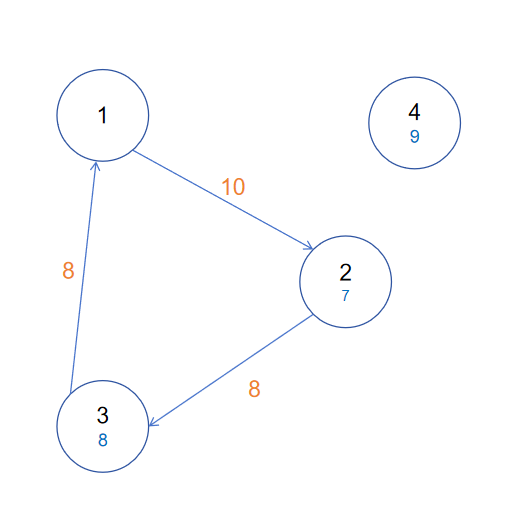
给出一种合法方案如下，选择k=8,即删去边3->1与2->3,接着增加边1->4及1->3